New version (June, 2020)

This is a new version of X-Ray Server's diffraction program launched in June-2020. The previous version is still available here for conservative users. However, when making a choice please consider the following benefits and features brought be this new version:

• Up to 10x faster calculations due to the reduction of the scattering matrix size. The original GID_sl was designed for Grazing Incidence X-ray diffraction (GID) where both incident and diffracted waves make small angles to the crystal surface and experience specular reflection. In this case the scattering matrix is 4x4, which corresponds to accounting for not only incident and diffracted waves, but also their specularly reflected counterparts. However, in the vast majority of calculations performed at X-Ray Server GID_sl is used for usual diffraction without the GID effects. In these cases the specularly reflected waves can be neglected and the scattering matrix can be reduced to the 2x2 size. Similarly, in the extremely asymmetric cases, whether grazing incidence or grazing exit, the scattering matrix can be made 3x3. The new version of GID_sl introduces the scattering matrix reduction parameter, which may have tree values: No (the old 4x4 behavior), Prescan and Fly. When the parameter is set to "Prescan", GID_sl examines all Bragg curve points for possible reduction and then applies the maximum found matrix size to all points. This option ensures there is no matrix size switch during the scan. With the "Fly" option, the matrix size is chosen individually for each point of the scan, which is the fastest. If all Bragg curve points are calculated with the 2x2 matrix the calculation time is reduced by approximately 10x compared to the 4x4 case.
   
• Option xhphase to specify phases for the Xh (Chi-h) parameters of the layers. This is mainly meant for very thin layers which may grow on substrates as e.g. either ABAB... or BABA... Note that xhphase differs from xhdf which is a phase shift between Xrh and Xih in non-centrosymmetric crystals. The phases are specified in the multiples of π and can be in the range [-2, 2]. Example: xhphase=1.
   
• Option to calculate X-ray Standing Waves (XSW) in crystals. One can calculate either the XSW at certain depth as a function of scan parameter (angle or energy) or a 2D-pattern as a function of scan parameter and the depth inside the crystal. Two modes are available: either the phase in π units of the probe point location with respect to the Bragg planes (0=in planes, 1=between the planes) or let the phase change with depth when the phase input is left blank or specified as "none".
   
• New calculation engine based on the ZGESV (LAPACK) and CPOLY (ACM) open-source routines.
   

Introduction

This page is a CGI interface to my program GID_sl simulating dynamical x-ray diffraction from strained crystals, multilayers, and superlattices. The name 'GID_sl' comes from the original aim of this program to simulate grazing incidence x-ray diffraction from multilayers and superlattices [1-3]. Later on, GID_sl was extended to extremely asymmetric geometries and usual Bragg-case [4]. At present this program is applicable to any coplanar and non-coplanar Bragg-case geometry with diffraction scans round arbitrary axes. 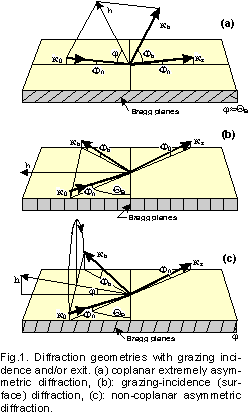Some typical examples of grazing-incidence geometries where the GID_sl can be used are shown on Fig.1.

The program can simulate the following profiles of structure parameters and defects in multilayers:

1. Normal lattice strains, da(z)/a;
2. Crystal polarizabilities x0(z), xh(z), [chi₀, chi_h] including the Debye-Waller profiles wh(z), w0(z);
3. Interface roughness sigma(z) in multilayers.

The effects of lateral strains (relaxed multilayers, misfit dislocations, etc) or crystal curvature are NOT simulated by this code. GID_sl is not aimed either for the truncation rod scattering (for very big deviations from Bragg peaks).

The program implements a "discrete" algorithm, i.e. the surface layer of crystal is subdivided onto "perfect" sublayers, each one possessing its own x0, xh, normal strain da/a, thickness t, and the rms height sigma of interface roughness. After solving the dynamical diffraction problem for each of the layers, the reflection from the whole system is calculated with the help of the (2x2) recursive matrix algorithm, RMA [6], which is a development of our earlier (4x4) transfer matrix approach, TMA [1-5]. While the TMA was an extension to the Abeles matrix solution [7] for x-ray specular reflection by multilayers, and the RMA can be viewed as a generalization of Parratt's and Bartels' recursive methods [8,9] for the specular reflection and non-grazing Bragg diffraction by multilayers respectively. The RMA works about 2 times slower than the TMA, but it is free of some principal divergencies which might happen with the TMA. In fact, GID_sl dynamically selects between the TMA and RMA depending on the conditions of calculations.

Acknowledgments: The idea of this X-ray Web Server appeared under the influence of excellent x-ray server by Eric Gullikson at the LBL. The solution to the plots outputs was prompted by William Lavender. Some ideas on making GID_sl user-friendly were suggested by Pavel Petrashen. I am grateful to all of my co-authors listed in the References below and to many others for the collaboration and helpful discussions resulted in the development of the TMA and RMA methods. Finally, since the server was launched, I have received a number of valuable comments and suggestions from many users. This response cannot be overestimated because it helps to improve the algorithms, extend the services and avoid possible bugs. Among many othes I am especialy grateful to Prof. Dr. Marius Grundmann for the communication helped to extend the calculations to larger strains and for comparing GID_sl with available commercial software [10].

1. S.A.Stepanov, "Method of transfer matrices and dynamical thick-crystal approximation in surface x-ray diffraction by multilayer structures", Crystallogr. Reports, 39 (1994) 182-187.
2. S.A.Stepanov, U.Pietsch and G.T.Baumbach, "A matrix approach to x-ray grazing incidence diffraction in multilayers", Z. Physik B, 96 (1995) 341-347.
3. S.A.Stepanov and R.Koehler, "Real-structure effects in the dynamical theory of grazing incidence x-ray diffraction", J. Appl. Phys., 76 (1994) 7809-7815.
4. S.A.Stepanov and R.Koehler, "A dynamical theory of extremely asymmetric x-ray diffraction taking account of normal lattice strain" , J. Phys. D: Applied Physics, 27 (1994) 1923-1928.
5. S.A.Stepanov, E.A.Kondrashkina, M.Schmidbauer, R.Koehler, J.-U.Pfeiffer, T.Jach, and A.Yu.Souvorov, "Diffuse scattering from interface roughness in grazing incidence x-ray diffraction", Phys. Rev. B, 54 (1996) 8150-8162.
6. S.A.Stepanov, E.A.Kondrashkina, R.Koehler, D.V.Novikov, G.Materlik, and S.M.Durbin, "Dynamical x-ray diffraction of multilayers and superlattices: Recursion matrix extension to grazing angles", Phys. Rev. B, 57, (1998) 4829-4841.
7. F.Abeles, Ann. Phys. (Paris), 3 (1948) 504; 5 (1950) 596.
8. L.G.Parratt, "Surface studies of solids by total reflection of x-rays", Phys. Rev., 95 (1954) 359-369.
9. W.J.Bartels, J.Hornstra and D.J.W. Lobeek, "X-ray diffraction of multilayers and superlattices", Acta Cryst. A, 42 (1986) 539-545.
10. M.Grundmann and A.Krost, "Atomic structure based simulation of X-ray scattering from strained superlattices", Phys. Stat. Sol. (b), 218 (2000) 417-423.

Program Guide

This short guide provides some explanations on the GID_sl data input and outlines the restrictions of this Web interface.

The GID_sl program is executed on a single PC, which runs a Web server under Windows operating system. Since this PC is shared by all X-ray Server users, there is a mechanism to restrict the maximum number of tasks processed at a time. If you unlikely hit that restriction, please try back later. Also, please, avoid overloading the server by submitting multiple tasks at the same time.

To obtain the results from GID_sl one needs to fill out the input form and click on the SUBMIT button. If the input is correct, the results will be presented as a figure and a reference to downloadable ZIP file containing the data and the listing of calculation parameters. Otherwise, an error message will be returned.

The specification of x-rays should not cause any problems. If mixed polarization is chosen, the results for σ- and π- polarizations are added with the weight contributions 1/(1+|cos(2*QB)|) and |cos(2*QB)|/ (1+|cos(2*QB)|), respectively. The weights are interchanged for the special case of scan which simulates GID takeoff spectra measured with position-sensitive detector (PSD). In these measurements the monochromator is turned by 90 degr. and it collimates the incidence angle instead of beam divergence in the Bragg plane.

The crystal substrate material is specified by the "crystal code" referring to the X0h database which is used for automatic calculation of the scattering and absorption factors x0 and xh (chi ₀ and chi _h) respectively. See the X0h page for more information on the scattering factors calculations. Here is the list of crystals currently available in the X0h database.

Then, "Reflection" stands for the Miller indices of the Bragg reflection; "Sigma" is the rms height of substrate roughness expressed in Angstrom; "W0" and "Wh" are the Debye-Waller like corrections to the values provided by the X0h database for x0 and xh respectively. Finally, "da/a" is the correction to the Bragg planes spacing (the X0h data are used as a reference value).

The geometry of Bragg diffraction can be specified by 9 different ways. Basically one has to distinguish between the coplanar diffraction cases (those where the incident wave vector k₀, the reciprocal lattice vector h, and the diffracted wave vector k_h lay in the same plane perpendicular to the surface -- Fig.1a) and the non-coplanar cases (Fig.1b,c) where the above condition is not satisfied, i.e. the scattering plane defined by k₀ and h is not perpendicular to the surface. The coplanar geometries are more commonly used in the x-ray experiments since they are simpler to implement. On the other hand, the non-coplanar geometries provide a greater flexibility in choosing the x-ray incidence and exit angles as well as in scanning around the Bragg peaks.

If one knows the orientation of crystal surface, then the coplanar diffraction cases (Fig.1a) can be specified as either grazing incidence, or grazing exit, or the symmetric Bragg case. In the latter case the Bragg planes must be chosen parallel to the surface.

Four simplified inputs are provided for coplanar diffraction geometries. Those do not require a knowledge of crystal surface orientation, but instead they expect one of the four parameters: either the incidence angle of k₀, or the exit angle of k_h, or disorientation angle of the Bragg planes, or the asymmetry factor beta=g₀/g_h. Use the SIMPLIFIED TEMPLATES below to access the new interfaces.

The non-coplanar cases (Fig.1b,c) always require the specification of crystal surface orientation and an additional parameter -- either the incidence or exit angle for the exact kinematical Bragg position (the actual position of the Bragg peak may deviate from the kinematical value due to refraction). The specification of additional angle is not required for symmetric non-coplanar cases (Fig.1c). The grazing incidence diffraction geometry (Fig.1b) as a particular case of non-coplanar geometries, always requires specifying the incidence or exit angle of x-rays. A common mistake is specifying GID as a symmetric Bragg case. Then, as one can see on Fig.1b, the incidence and exit angle will be taken zero. This happens because GID is a symmetric Laue case, not the Bragg one, and the wave yielding the crystal in GID is a specular component of diffracted wave, not the real one.

For more details on the specification of coplanar and non-coplanar geometries to GID_sl click here.

Here are some examples for GaAs crystal with the (001) surface plane specified:

• The (004) reflection can only be specified as a symmetric Bragg case (there is no choice).
   
• Reflection (113) can be specified as an extremely asymmetric coplanar case with grazing incidence. For E=8.5 keV this gives the incidence angle of 0.09 degr.
   
• If a higher incidence angle is required, one can proceed to non-coplanar case and select the incidence angle equal to e.g. 1.00 degree.
   
• Finally, the same (113) plane can be brought into the symmetric non-coplanar geometry (in this case the incidence and exit angles will be equal to 22.77 degr.)
   

The crystal surface orientation (if needed) is specified via the indices of external surface normal, the angle and the direction of maximum miscut. Please, do not specify non-integer indices if the miscut direction does not coincide with some crystallographic axis: use an integer approximation instead. Example: enter (111 322 4) instead of (1.11 3.22 0.04).

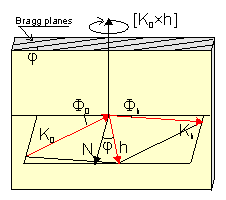The scan axis for coplanar cases is usually a vector perpendicular the scattering plane and parallel to the surface. Such a vector can be presented as [k0 x h] or [k0 x N_surface] -- Fig.2. For the grazing incidence diffraction (Fig.1b) the scan vector is usually N_surface (the crystal is rotated round the surface normal). GID_sl can also simulate the special case of GID where the incidence beam is not collimated in the Bragg plane and the sample is not scanned. Instead of scanning, the diffraction curve is recorded by PSD. For other non-coplanar cases there is a choice of several "natural" scan axes, or an arbitrary axis can be specified (please, use integer indices).

The scan range is that around the Bragg peak along chosen scan axis. The GID_sl allows plotting the diffraction curve depending on the scan angle, the incidence angle, or the exit angle. However, in all of the cases one has to specify the scan range as the deviations from the Bragg peak. It is a frequent mistake when users request the plot depending on the incidence angle of x-ray and then attempt to specify the incidence angles in the scan range fields.

The alpha_max tells GID_sl at what Bragg deviations alpha=((k0+h)^2-k0^2)/k0^2 it can stop accounting for diffraction in layers and switch to an amorphous layer model. At large deviations from the Bragg condition the diffracted wave intensity is very weak and trying to account for this tiny effect may lead to loss of precision in the calculations. It is recommended to leave this parameter unchanged unless you experience some numerical errors.

The scattering matrix reduction parameter allows GID_sl to reduce the scattering matrix size from 4x4 when either the incident or the diffracted wave or both are not grazing. It may speed speedup calculation up to 10 times and improve stability by not trying to account for very weak effects along with the strong ones. This parameter may have tree values:

• No which means always use 4x4 scatting matrix where all specular waves are taken into account. This corresponds to the behavior of the previous version of GID_sl.
• Prescan instructs GID_sl to examine all Bragg curve points for possible reduction and then apply the maximum found matrix size to all points. This option ensures there is no matrix size switch during the scan.
• Fly instructs GID_sl to choose the matrix size individually for each point of the scan. The size may be chosen as 4x4, 3x3, and 2x2. This is the fastest and the default.

Along with the Bragg curves, GID_sl can also optionally calculate X-ray Standing Waves (XSW) in the layers (see an XSW template below). It can calculate either the XSW curves as a function of the scan angle or the maps with the depth inside the crystal as the second coordinate. While most of the XSW parameters are probably self-explanatory, the Location phase parameter is the location of probe point with respect to the Bragg planes measured in π: when phase=0 the probe is located in the planes and when phase=1 the probe is located midway between the planes. When the phase is not specified, it is taken varying with the depth coordinate z.

The specification of crystal surface layer profile is implemented with a simple scripting language. A typical syntax is:

; comments are allowed in any line, but should
; not contain special symbols like '"*?$!@%
period=5
t=10 x0=(5e-4,7e-6) xh=(3e-4,5e-6) xhdf=1. w0=1, da/a=2e-4
t=10 code=GaAs x=0.3 code2=AlAs x2=0.7 da/a=auto sigma=2
t=10 code=InAs xhpase=1
t=10 wh=.5 da/a=2e-4 sigma=2
t=10 da/a=2e-4
t=10
end period

-- where:

• ";" and "!" are the comment signs. The lines starting with these symbols are ignored and if these symbols are present at the middle of a line, everything to the right of them is ignored too.
• "period=" and "end period" mark the beginning and the end of a periodic group of layers. The maximum of two enclosed periods is allowed.
• "t=10" is the layer thickness in Angstroms. NOTE: this is the only parameter of layer which cannot be skipped.
• "code=" is a code of material in the X0h database. Use this code for automatic calculation of layers x0 and xh (chi₀ and chi_h). For the reference of available codes see the menu for the substrate. Please, be advised that the codes are case sensitive (while the script keywords are not).
  If none code is specified, the substrate code is used by default.
  NOTE: the choice of crystal code does not affect the value of lattice spacing in the layer used by GID_sl. Initially, the Bragg spacings for all the layers are set equal to that in the substrate and their variation is solely specified through the parameter "da/a".
• "x=",   "code2=",   "x2=",   "code3="   are the parameters to specify composite materials and solid solutions. For example, a structure like Ga_0.3Al_0.7As can be specified as: "code=GaAs x=0.3 code2=AlAs", or even shorter: "x=0.3 code2=AlAs". One can also specify "x2=0.7", but this is redundant, because the program automatically takes care of the sum of all "xN" being equal to one (e.g. the input like "x2=0.8" in the above example would cause an error message). Maximum of 4 codes are allowed and all of them must be valid ones in the X0h database.
• "x0=" and "xh=" are the layer chi₀ and chi_h. These parameters, when specified, replace the data given by the X0h database.
• "xhdf=" is the difference in the phases of real and imaginary parts of chi_h (in the multiples of π). This is an additional data for "xh=" in the case of non-centrosymmetric crystals. For centrosymmetric crystals one has either xhdf=0, or xhdf=1 (depending on the Bragg reflection).
• "w0=" and "wh=" are Debye-Waller-like factors for x0 and xh. They may be used to correct the x0 and xh values provided by the X0H database:

    x0=w0*x0
    xh=wh*xh
  

  By default, these factors are equal to one. Unlike the usual Debye-Waller factors, w0 and wh can be greater than one, because they simply provide one more way to specify x0 and xh.
  HINT: use wh=0 to specify amorphous layers (e.g. surface oxide films) or the layers where Bragg planes are very far from the Bragg condition.
• "da/a=" is the relative variation on perpendicular lattice spacing in the layer with respect to the reference value (which is usually the value in the substrate). The specification "da/a=a" or "da/a=auto" causes the automatic calculation of da/a of the layer with respect to the substrate via the difference of the free-state lattice parameters of the substrate and the layer and the Poisson ratio for the layer. In this case the layer must be specified by a code in the X0h database (or several codes in the case of a composite layer). The automatic calculation can be used for cubic structures only, since for the other structure symmetries the Poisson ratio is not relevant.
  The formula used for automtic calculation of da/a with given Poisson ratio "p" is:

    da/a = ((1+p)/(1-p)) * (a_-a_substrate)/a_substrate
  

  where "a" is the lattice parameter of "free standing" material as given by the X0h database.
• "sigma=" is the rms roughness at the upper layer interface expressed in Angstroms. This value should not exceed the layer thickness. Besides, the values of sigma > 5A should be used with care, since GID_sl accounts for roughness with a method [3] similar to that by Nevot and Croce, which presumes small roughness.
• "xhphase=" specifies phase for the material susceptibility Xh (Chi-h) of layer. This is aimed for very thin layers which may grow on substrates as e.g. either ABAB... or BABA... Note that "xhphase" differs from "xhdf" which is a phase shift between Xrh and Xih in non-centrosymmetric crystals. The phases are specified in the multiples of π and can be in the range [-2, 2].

Here is a practical example -- a profile for 20-period AlAs/GaAs superlattice with 100 Angstroms of GaAs and 70 Angstroms of AlAs in each period; the structure is covered by additional 200A of GaAs and, finally, there is some 20A amorphous oxide layer on the surface:

; Oxide layer:
t=20. w0=0.7 wh=0.
; -- w0=0.7 because of reduced layer density
; -- wh=0 since the layer is amorphous

; Cap layer:
t=200.
; -- when code is not specified, then
; the substrate code (GaAs) is used

; Superlattice:
period=20
  t=100.
  t=70. code=AlAs da/a=2.775e-3
  ; The strain value is taken from Bocchi et al.,
  ; J.Cryst.Growth, 132 (1993) 427
end period

For the rest of parameters users are suggested to follow their common sense. To ensure that the input was correct, please verify respective listing file -- a file with the ".TBL" extension in the ZIPped archive returned by GID_sl.

Access to GID_sl

To simplify understanding the GID_sl interface, users are provided with the templates listed below. All of the templates link to the same program and provide the same functionality (except for the simplified templates which are designed for coplanar diffraction only). The templates differ by preloaded data to demonstrate some possible applications of the GID_sl.

When submitting the GID_sl task, it is possible to check the progress watching option. The progress watching is obviously more comfortable, but it might not work with some old Web browsers. Also, it is a bit slower because of putting an additional load on the network and launching each 5 seconds a status query program on my computer. Welcome to try both of the ways and choose the most convenient for your needs.

Retrieve results

Here is a tool to retrieve the results of finished jobs if you know the job ID. Some possible uses of this tool are:

1. You started a job with the progress watch option; the server returned the job ID and began reporting the progress. However, you found that the calculations would take too long. Then, you may break the connection and retrieve the data later on with this tool. If the calculations are not finished, the tool will resume the watch process.
2. The data are accidentally deleted from your client computer and you want another copy of them. In this case you should be aware that results are usually stored on the server for about one day after respective job is finished.

Site navigation: Home page X-ray scattering factors (X0h) Search for X-ray Bragg planes (X0h-search) X-ray Bragg diffraction (GID_sl) X-ray specular reflection (TER_sl) X-ray scattering from roughness (TRDS_sl) X-ray resonant reflection (MAG_sl) X-ray Multiple Bragg diffraction (BRL)